Unit Circle Csc Sec Cot

What is Unit Circle?

In the world of calculus, pre-calculus, and trigonometry, you will ofttimes find reference toward and problems regarding "the unit circle." Just, oddly, we are rarely ever taught what information technology is!

In simple terms, the unit circumvolve is a mathematical tool for making the employ of angles and trigonometric functions easier. By understanding and memorizing "the unit circle" we are able to cakewalk through otherwise calculation-heavy problems, and make our lives a whole lot easier.

The unit circle, in it's simplest form, is really exactly what it sounds similar: A circumvolve on the Cartesian Airplane with a radius of exactly $1 unit of measurement$ . Like this bare unit circle below:

Blank unit circle with radius of i

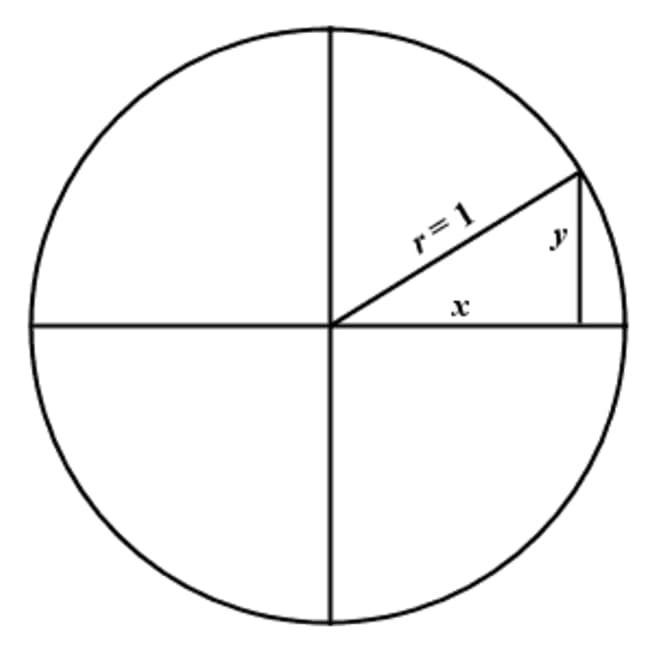
Next, by filling in this unit of measurement circle with normally used angles and evaluating these angles with sine and cosine, we go something a $little$ more complicated:

Sine and Cosine evaluated angles of unit circle

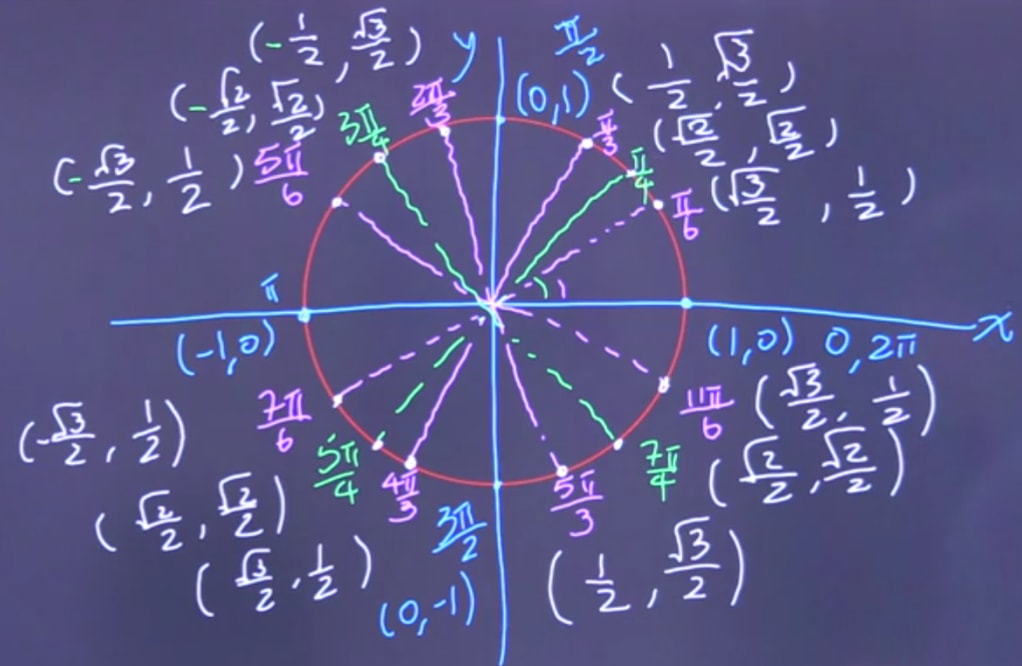
Scared? Don't be. This epitome might seem intimidating, but when we break it downward it more than coherent parts, patterns offset to emerge.

Unit Circle With All 6 Trig Functions Nautical chart:

Instead of referring to that intimidating image above, allow'southward simplify the unit circumvolve with $\sin \cos \tan \sec \csc$ and $\cot$ in a nice trivial chart:

Nautical chart of simplified unit circumvolve with sin cos tan sec csc and cot

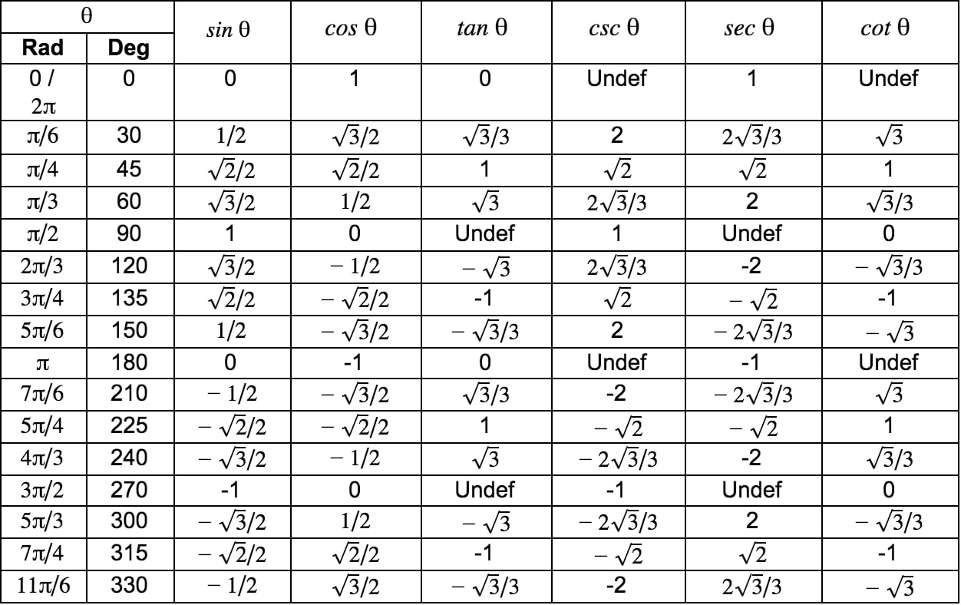
This above unit circle table gives all the unit circle values for all iv unit of measurement circle quadrants. Equally you lot can see, listed are the unit circle degrees and unit circle radians. You lot should know both, only you're most likely to be solving problems in radians. Now, the next natural question is, how tin can I remember the unit circumvolve?

How to Memorize the Unit Circle:

Memorizing the unit circle is actually much easier than you'd think, thank you to a couple petty tricks:

Fox 1:

Because of the following 4 equations, nosotros only need to memorize the unit circle values for sine and cosine.

$\tan \theta = \frac{\sin \theta}{\cos \theta}, \cot \theta = \frac{\cos \theta}{\sin \theta}, \sec \theta = \frac{1}{\cos \theta}, \csc \theta = \frac{ane}{\sin \theta}$

With these 4 equations, we don't even need to memorize the unit of measurement circumvolve with tangent!

Trick 2:

Past knowing in which quadrants x and y are positive, nosotros only need to memorize the unit of measurement circle values for sine and cosine in the starting time quadrant, as the values only change in their sign. To use this trick, in that location are a few things we need to understand first:

i) The first important matter to note is what values sine and cosine give us on the unit circle. Because of SOHCAHTOA, nosotros know this:

$\sin \theta$ gives usa the Y-coordinate and $\cos \theta$ gives us the Ten-coordinate

ii) Now looking at each quadrant:

Quadrant 1: Ten is Positive, Y is Positive

Quadrant 2: 10 is Negative, Y is Positive

Quadrant three: X is Negative, Y is Negative

Quadrant 4: X is Positive, Y is Negative

3) Side by side, looking at where each quadrant lies:

Quadrant 1: 0 – $\frac{\pi}{ii}$

Quadrant 2: $\frac{\pi}{two} - \pi$

Quadrant 3: $\pi$ – $\frac{3\pi}{two}$

Quadrant 4: $\frac{3\pi}{2} - 2\pi$

iv) The value of sine and cosine will e'er be "the same" for the same denominator:

$\sin \frac{\pi}{iii} = \frac{\sqrt{three}}{2} and \sin \frac{4\pi}{3} = -\frac{\sqrt{three}}{ii}$

With these tricks in mind, the procedure of how to call back the unit circle becomes and then much easier!

How to Use the Unit of measurement Circumvolve:

The all-time way to go comfy with using the unit of measurement circumvolve is to do some unit circle practise.

Example 1:

Find $\sin \frac{four\pi}{3}$

Footstep 1: Identify The Quadrant

Since we're dealing with sine, which we will somewhen take memorized, all we need to exercise is figure out what quadrant we're in then we know whether our answer volition be positive or negative.

Since:

$\frac{3\pi}{2} > \frac{4\pi}{iii} > \pi$

We are therefore in the 3rd quadrant. Thus, since sine gives us the y coordinate, and we are in the third quadrant, our answer volition be negative!

Step 2: Solve

The next step is simple – using what we've memorized, we can easily solve this problem.

$\sin \frac{4\pi}{three}$ = - $\frac{\sqrt{3}}{2}$

Example 2:

Find $\tan \pi$

Step ane: Place The Quadrant

Since we're dealing with the unit circle with tan, we will need to use the values we've memorized from sine and cosine, and then solve. First, all the same, we need to figure out what quadrant we're in then we know whether our answers for sine and cosine will be positive or negative.

Since:

$\frac{3\pi}{2} > \pi > \frac{\pi}{2}$

We are therefore in between the second and third quadrant on the x-centrality. Since sine gives us the y coordinate, and we are on the x-axis, our answer will really be zero! As well, since cosine gives us the x-coordinate, and we are in betwixt the second and third quadrant (where cosine is negative for both), our answer will exist negative!

Footstep two: Solve

The adjacent step is elementary – using what we've memorized, we tin can hands solve this problem. But in this case, we demand 1 extra pace. We must utilise the equation for tangent discussed earlier in trick i, assuming we oasis't memorized the values for tangent on the unit circle.

$\tan \theta = \frac{\sin \theta}{\cos \theta} = \frac{0}{-ane} = 0$

Example 3:

Discover $\csc \frac{\pi}{6}$

Step 1: Identify The Quadrant

Since we're dealing with cosecant, it is important to recognize nosotros will need to utilise sine values to solve using the equation for cosecant discussed earlier in play tricks ane. Starting time, all the same, we demand to figure out what quadrant we're in then we know whether our reply for sine volition exist positive or negative.

Since:

$\frac{\pi}{2} > \frac{\pi}{six} > 0$

Nosotros are therefore in the first quadrant. Thus, since sine gives the states the y coordinate, and we are in the get-go quadrant, our reply will be positive!

Footstep 2: Solve

The next stride is simple – using what we've memorized, we can easily solve this problem. Simply in this example again, we need i extra stride. We must use the equation for cosecant discussed before in play a joke on one, bold we oasis't memorized the values for cosecant on the unit circle.

$\csc \frac{\pi}{six} = \frac{1}{\sin \frac{\pi}{6}} = \frac{ane}{0.five} = ii$

Now that nosotros've washed some practice, do some more on your own! In no fourth dimension at all, you'll exist gear up for any upcoming unit circumvolve quiz.

Unit Circle Csc Sec Cot,

Source: https://www.studypug.com/trigonometry-help/unit-circle

Posted by: mossstrater.blogspot.com

Share this post